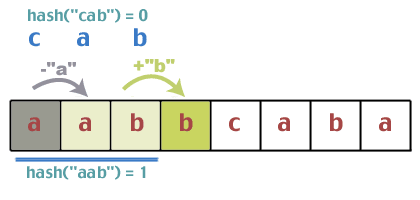String Matching Algorithms

The problem of matching patterns in strings is central to database and text processing applications. The problem will be specified as: given an input text string t of length n, and a pattern string p of length m, find the first (or all) instances of the pattern in the text.

We’ll refer to the ith character of a string s as s[i] (this syntax makes a lot of sense if you think of a string as an array of characters).

Brute force

The simplest algorithm for string matching is a brute force algorithm, where we simply try to match the first character of the pattern with the first character of the text, and if we succeed, try to match the second character, and so on; if we hit a failure point, slide the pattern over one character and try again. When we find a match, return its starting location.

Java code for the brute force method:

for (int i = 0; i < n-m; i++) {

int j = 0;

while (j < m && t[i+j] == p[j]) {

j++;

}

if (j == m) return i;

}

System.out.println(‘‘No match found’’);

return -1;

The outer loop is executed at most n-m+1 times, and the inner loop m times, for each iteration of the outer loop. Therefore, the running time of this algorithm is in O(nm).

Boyer-Moore

On first glance, one might think that it is necessary to examine every character in t in order to locate p as a substring. However, this is not always necessary, as we will see in the Boyer-Moore algorithm. The one caveat for this algorithm is that it works only when the alphabet (set of possible elements of strings) is of a fixed finite size. However, given that this is the case in the vast majority of applications, the Boyer-Moore algorithm is often ideal. As we will see, it works fastest when the alphabet is not too large and the pattern is fairly long (i.e. not many orders of magnitude shorter than the input).

The key to not examining every character in the text is to use information learned in failed match attempts to decide what to do next. This is done with the use of precomputed tables, as we will see shortly.

Perhaps the most suprising feature of this algorithm is that its checks to see if we have a successful match of p at a particular location in t work backwards. So if we’re checking to see if we have a match starting at t[i], we start by checking to see if p[m-1] matches t[i+m-1], and so on.

The reason for this backwards approach is so we can make more progress in case the attempted match fails. For example, suppose we are trying to match the pattern “ABCDE” at position i of the input t. but at t[i+4], we find the character ’X’. ’X’ doesn’t appear anywhere in “ABCDE”, so we can skip ahead and start looking for a match at t[i+5], since we know that the ’X’ prevents a match from occurring any earlier. In order to get the information that we need out of each failed match,  the algorithm pre-processes the input pattern p and generates tables (some- times called “jump tables”, since they indicate how far ahead in the text to “jump”). One table calculates how many positions to slide ahead in t based on the character that caused the match attempt to fail, and the other makes a similar calculation based on how many characters were matched successfully before the match attempt failed.

The first table is easy to calculate: Start at the last character of the search string with a count of 0, and move towards the first character; each time you move left, increment the count by 1, and if the character you are on is not in the table already, add it along with the current count (so, e.g., you could use a hash table with characters as keys and the “shifts” that you are calculating as values). All other characters (those not appearing in p) receive a count equal to the length of the search string. (Here we see why a fixed finite alphabet is essential.)

For example, for the search string ABCABDAB, this “shift” table is:

Character             Shift

B                             0

A                             1

D                             2

C                             5

all other chars        8

The second table is slightly more difficult to calculate: for each value of i less than m, we must first calculate the pattern consisting of the last i characters of the search string, preceded by a mis-match for the character before it; then we must find the least number of characters that partial pat- tern can be shifted left before the two patterns match. This table is how we account for the possible repetitions within the search string.

For example, for the search string ABCABDAB, the “skip” table is:

i           Pattern           Shift

0          B                         1

1          AB                      8

2          DAB                   3

3          BDAB                 6

4          ABDAB              6

5          CABDAB           6

6          BCABDAB        6

7          ABCABDAB     6

Here is some pseudocode for this algorithm, supposing that the preprocess- ing to generate the tables has already been done.

public int BoyerMoore(String t, String p) {

int n = t.length();

int m = p.length();

int i = 0;

while (i <= n - m) {

int pos = m - 1;

while(p[pos] == t[i+pos]) {

if(pos == 0) { return i; }

pos--;

}

i += max (skip((m-1)-pos) , pos - ((m-1) - shift(t[pos+i])) )

}

print(‘‘pattern not found’’);

return -1;

The preprocessing to generate the tables takes Θ(m + σ) time, where σ is the size of the alphabet (one pass through p, plus adding an entry for each other char in the alphabet), and Θ(σ) space. We could reduce these both to Θ(m), but at the expense of the constant- time access that we enjoy with the current implementation (since it would then take m time to search for a character not in the table).

The best and average-case performance of this algorithm is O(n/m) (since only 1, or some small constant number out of every m characters of t needs to be checked). So, somewhat counter-intuitively, the longer that p is, the faster we will likely be able to find it.

The worst-case performance of the algorithm is approximately O(nm). This worst case occurs when t consists of many repetitions of a single character, and p consists of m − 1 repetitions of that character, preceded by a single instance of a different character. In this scenario, the algorithm must check n − m + 1 different offsets in the text for a match, and each such check takes m comparisons, so we end up performing just as many computations as for the brute-force method.

In practice, in typical string-matching applications, where the alphabet is large relative to the pattern size, and long repetitions of a single character or a short pattern of characters is not likely, Boyer-Moore performs very well.

Karp-Rabin

The Karp-Rabin algorithm searches for a pattern in a text by hashing. So we preprocess p by computing its hashcode, then compare that hash code to the hash code of each substring in t. If we find a match in the hash codes, we go ahead and check to make sure the strings actually match (in case of collisions). Code for the algorithm:

public int KarpRabin(String t, String p) {

int n = t.length();

int m = p.length();

int hpatt = hash(p);

int htxt = hash(t[0..m-1]);

for(int i = 0; i < n; i++) {

if (htxt == hpatt) {

if (t[i..i+m-1] == p) { return i; }

htxt = hash(t[i+1..i+m]);

}

}

System.out.println(‘‘not found!’’);

return -1;

}

For efficiency, we want to be able to quickly compute hash(t[j+1...j+m]) from hash(t[j...j+m-1]) and t[j+m] (instead of naively computing the hash from scratch for every substring of t - this would take O(m) time, and since it is done on each loop, we would have total time of O(mn)). Hash functions for which we can compute in this more efficient way are called rolling hashes.

The best-case and average-case time for this algorithm is in O(m + n) (m time to compute hash(p) and n iterations through the loop). However, the worse case time is in O(mn), which occurs when we have the maximum number of collisions - every time through the loop, we find that the hashes match, but the strings don’t. With a good hashing function, this is unlikely.

Karp-Rabin is inferior for single pattern searching to many other options because of its slow worst-case behavior. However, it is excellent for multiple pattern search. If we wish to find one of some large number, say k, fixed- length patterns in a text, we can make a small modification that uses a hashtable or other set to check if the hash of a given substring of t belongs to the set of hashes of the patterns we are looking for. Instead of computing one pattern hash value hpatt, we compute k of them and insert them into a hashtable or other quick lookup structure. Then, instead of checking to see if htxt == hpatt, we check to see if htxt is in the table we built. In this way, we can find one of k patterns in O(km + n) time (km for hashing the patterns, n for searching).