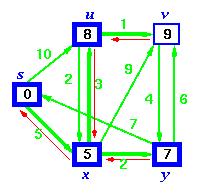
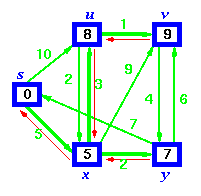
Dijkstra's Algorithm solves the single-source shortest path problem in weighted graphs. Here we show it running on a planar graph whose edge weights are proportional to the distance between the vertices in the drawing -- thus the weight of an edge is equal to its visible length.
Dijkstra's algorithm starts from a source node, and in each iteration adds another vertex to the shortest-path spanning tree. This vertex is the point closest to the root which is still outside the tree. Watch as the tree grows by radiating out from the root. Note that it is not a breadth-first search; we do not care about the number of edges on the tree path, only the sum of their weights.
Dijkstra(G, w, s)
Initialize-Single-Source(G, s);
S<-- {}; Q <-- V[G];
while Q not equal {}
do u = extract-min(Q)
S = S U {u}
for each vertex v E Adj[u]
do relax(u, v, w)
Example: Step by Step operation of Dijkstra algorithm.
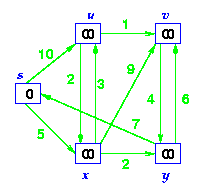
Step1. Given initial graph G=(V, E). All nodes nodes have infinite cost except the source node, s, which has 0 cost.
Step 2. First we choose the node, which is closest to the source node, s. We initialize d[s] to 0. Add it to S. Relax all nodes adjacent to source, s. Update predecessor (see red arrow in diagram below) for all nodes updated.
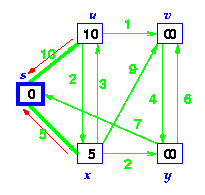
Step 3. Choose the closest node, x. Relax all nodes adjacent to node x. Update predecessors for nodes u, v and y (again notice red arrows in diagram below).
Step 4. Now, node y is the closest node, so add it to S. Relax node v and adjust its predecessor (red arrows remember!).
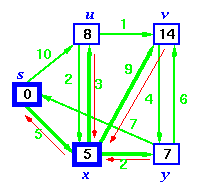
Step 5. Now we have node u that is closest. Choose this node and adjust its neighbor node v.
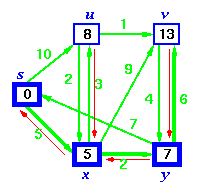
Step 6. Finally, add node v. The predecessor list now defines the shortest path from each node to the source node, s.
Q as a linear array
EXTRACT_MIN takes O(V) time and there are |V| such operations. Therefore, a total time for EXTRACT_MIN in while-loop is O(V2). Since the total number of edges in all the adjacency list is |E|. Therefore for-loop iterates |E| times with each iteration taking O(1) time. Hence, the running time of the algorithm with array implementation is O(V2 + E) = O(V2).
Q as a binary heap ( If G is sparse)
In this case, EXTRACT_MIN operations takes O(lg V) time and there are |V| such operations.The binary heap can be build in O(V) time.Operation DECREASE (in the RELAX) takes O(lg V) time and there are at most such operations.
Hence, the running time of the algorithm with binary heap provided given graph is sparse is O((V + E) lg V). Note that this time becomes O(ElgV) if all vertices in the graph is reachable from the source vertices.
Q as a Fibonacci heap
In this case, the amortized cost of each of |V| EXTRAT_MIN operations if O(lg V).
Operation DECREASE_KEY in the subroutine RELAX now takes only O(1) amortized time for each of the |E| edges.
As we have mentioned above that Dijkstra's algorithm does not work on the digraph with negative-weight edges. Now we give a simple example to show that Dijkstra's algorithm produces incorrect results in this situation. Consider the digraph consists of V = {s, a, b} and E = {(s, a), (s, b), (b, a)} where w(s, a) = 1, w(s, b) = 2, and w(b, a) = -2.
Dijkstra's algorithm gives d[a] = 1, d[b] = 2. But due to the negative-edge weight w(b, a), the shortest distance from vertex s to vertex a is 1-2 = -1.